K-means的一些讲解
k 均值算法


步骤
- 随机选取样本作为初始均值向量(初始值:k 的值【即几个簇】)(也可以不用样本点)
- 分别计算每个样本点到初始均值向量的距离(数据做了标准化),距离哪个点最近就属于哪个簇
- 每个簇重新计算中心点,重复第二步直到收敛
- 找到质心和离某个质心距离最近的点就分为一类。
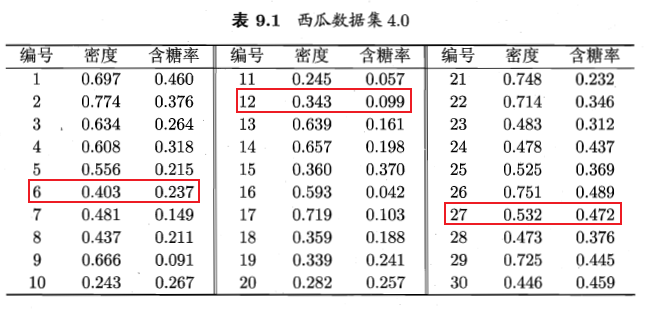

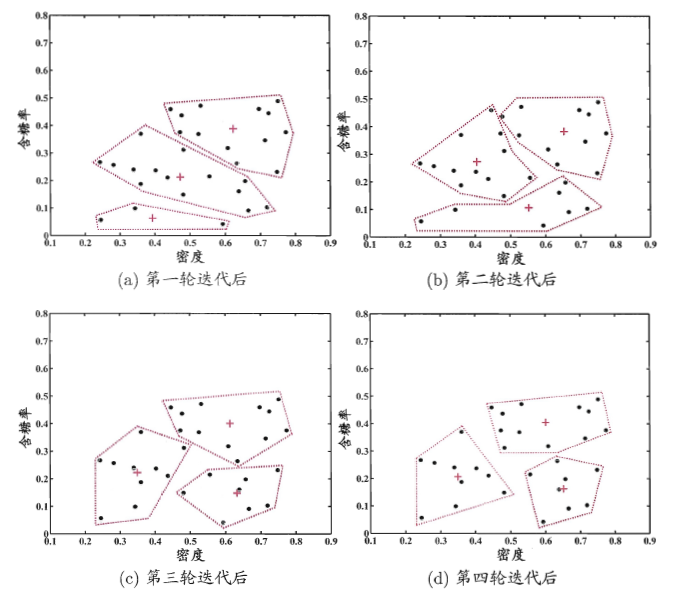
问题:需要指定k值,难以确定k值。
确定k值
1.手肘法
手肘法的核心指标是SSE(sum of the squared errors,误差平方和),
$$S S E = \sum _ { i = 1 } ^ { k } \sum _ { p∈m_i }| p - m _ {i } | ^ { 2 }$$
其中,Ci是第i个簇,p是Ci中的样本点,mi是Ci的质心(Ci中所有样本的均值),SSE是所有样本的聚类误差,代表了聚类效果的好坏。
手肘法的核心思想是:随着聚类数k的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。并且,当k小于真实聚类数时,由于k的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当k到达真实聚类数时,再增加k所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着k值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的k值就是数据的真实聚类数。当然,这也是该方法被称为手肘法的原因。

2. 轮廓系数法
思想:簇内样本的距离越近,簇间样本距离越远,平均轮廓系数越大,聚类效果越好。
该方法的核心指标是轮廓系数(Silhouette Coefficient),某个样本点Xi的轮廓系数定义如下:
$$S = \frac { b - a } { m a x ( a , b ) }$$
其中
a是Xi与同簇的其他样本的平均距离,称为凝聚度
b是Xi与最近簇中所有样本的平均距离,称为分离度。
最近簇的定义是,簇间不相似,最近的不相似
$$C _ { j } ={ a r g } m i n \frac { 1 } { n } \sum _ { p ∈c _ { s } } | p - X _ { i }| ^ { 2 }$$
其中p是某个簇Ck中的样本。事实上,简单点讲,就是用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后,选择离Xi最近的一个簇作为最近簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。
平均轮廓系数的取值范围为[-1,1]。
那么,很自然地,平均轮廓系数最大的k便是最佳聚类数。